Les formules électroniques
Le but de cette section est de montrer le strict minimum à connaitre du point de vue théorique pour comprendre et réaliser des circuits électroniques (il faut bien un peu de maths ![]() ).
).
Lois
Résistance
\[U = R \times I\]$U \Rightarrow$ Tension exprimée en Volts ($V$)
$I \Rightarrow$ Intensité exprimée en Ampères ($A$)
$R \Rightarrow$ Résistance exprimée en Ohms ($\Omega$)
La tension est constante lorsqu’un circuit est monté en parallèle. La tension se divise lorsque le circuit est monté en série.
L’intensité se divise lorsqu’un circuit est monté en parallèle. L’intensité est constante lorsqu’un circuit est monté en série.
Charge d’un condensateur
\[T = R \times C\]$T \Rightarrow$ Temps exprimé en secondes
$R \Rightarrow$ Résistance exprimée en Ohms ($\Omega$)
$C \Rightarrow$ Capacité du condensateur exprimée en Farads ($F$)
La courbe de charge est asymptotique. Après le temps $T$, le condensateur est chargé à 70 %. Après un temps $T$ supplémentaire, il est chargé de 70 % + (70 % des 30 % restant). etc. Un condensateur ne sera donc jamais chargé au maximum.
Un condensateur de $1 F$ serait composé de deux plaques de cuivre d’un mettre carré chacune espacées d’un millimètre.
Un condensateur de $1 µF$ au Tantal peut être remplacé par un condensateur de $10 µF$ électrochimique.
Tension efficace
\[V_{max} = V_{eff} \times \sqrt 2 \iff V_{eff} = \frac{V_{max}}{\sqrt 2}\]$V_{max} \Rightarrow$ Tension maximale exprimée en Volts ($V$)
$V_{eff} \Rightarrow$ Tension efficace exprimée en Volts ($V$)
Attention : Dans les analyses de tensions sur le circuit, il convient d’utiliser la tension maximale. Par exemple un transformateur 12 Veff aura une tension maximale d’environ 16,97 Vmax.
Puissance
\[P = U \times I\]$P \Rightarrow$ Puissance exprimée en Watts ($W$)
$U \Rightarrow$ Tension expriméee en Volts ($V$)
$I \Rightarrow$ Intensité exprimée en Ampères ($A$)
La calcul de la puissance dissipée par un composant est donc :
$P = (V_{e} – V_{s}) \times I$
Avec $V_{e}$ la différence de potentielle en entrée du composant et $V_{s}$, la différence de potentielle en sortie du composant.
Exemple avec un stabilisateur de tension (LM317) :
$V_{e} = 12 \times \sqrt 2 \, soit \, environ \, 17 V$
$V_{s} = 1,25 V \, à \, 17 V$
$I = 1 A$ (c’est la valeur maximale supportable du pont de diode utilisée dans mon alimentation stabilisée)
$=> P_{min} = (17 – 17) \times 1 = 0 W$
$=> P_{max} = (17 – 1,25) \times 1 = 15,75 W$
NOTE : Si la puissance dépasse $1 W$, il faut placer un dissipateur thermique.
Dissipation thermique
Prenons l’exemple d’un composant qui doit délivrer une puissance max de $15,75 W$ à température ambiante.
J’utilise personnellement une formule de calcule simplifiée : $R_{th} = \frac{(T_{j} – T_{a})}{P_{d}}$
$R_{th} \Rightarrow$ Résistance thermique exprimée en °C/W
$T_{j} \Rightarrow$ Température de jonction exprimée en °C. Cette valeur est spécifié par le constructeur (125°C pour le LM317; Donc 100°C pour avoir de la marge)
$T_{a} \Rightarrow$ Température ambiante exprimée en °C. Prendre 55°C (ça arrive plus souvent qu’on ne le croit)
$P_{d} \Rightarrow$ Puissance dissipée exprimée en Watts. Prendre une marge de sécurité (disons +25 %)
On obtient donc : $R_{th} = \frac{(100 – 55)}{16,2} = 2,77°C/W$
Il faut donc un radiateur à dissipation thermique d’au plus $2,77°C/W$. Une valeur en dessous fonctionnera très bien (car moins de résistance de dissipation).
Règles générales
Stabilisation d’un circuit
Le condensateur électrochimique utilisé pour stabiliser un circuit génère des interférences (self) qui sont contrecarrées par la mise en place d’un condensateur papier (ou céramique) de $0,1µF (=100nF)$ en parallèle du condensateur électrochimique.
Ces perturbations ne sont jamais visibles dans les logiciels d’analyse car ils considèrent toujours que les composants utilisés sont “« “parfaits”.
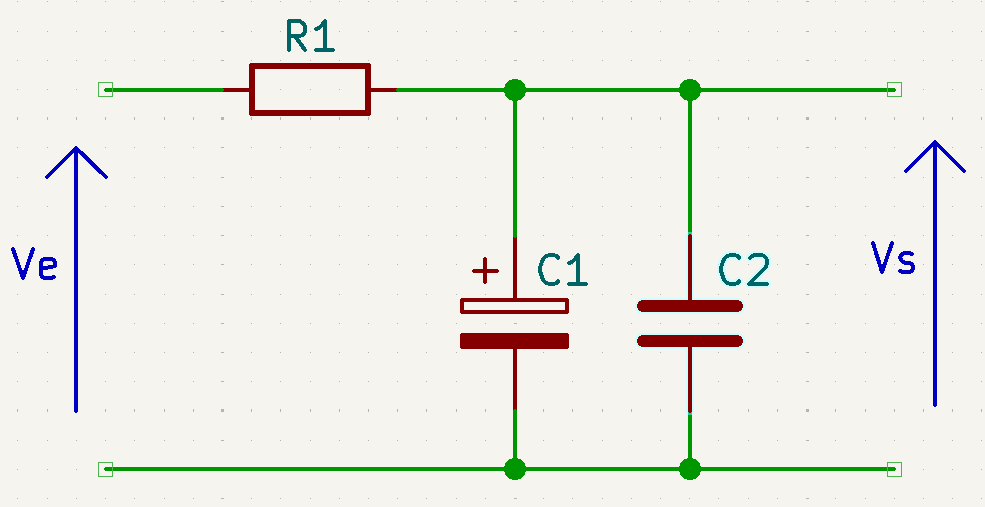
Le condensateur de stabilisation ne doit jamais être monté directement en parallèle de l’alimentation. Il faut utiliser une résistance comme le montre le schéma suivant :
$V_{e} \Rightarrow$ Tension d’entrée expriméee en Volts ($V$)
$R \Rightarrow$ Résistance de protection exprimée en Ohms ($\Omega$)
$C1 \Rightarrow$ Condensateur de stabilisation exprimée en Farad ($F$) - En général un condensateur électrolytique
$C2 \Rightarrow$ Condensateur dit de “découplage” pour supprimer les interférences exprimée en Farad ($F$) - En général en condensateur papier
$V_{s} \Rightarrow$ Tension de sortie expriméee en Volts ($V$)
Attention à la résistance qui réduit obligatoirement le courant dans le circuit protégé.
Quelques valeurs significatives :
| $V_{e}$ | $R$ | $C1$ | $V_{s}\,\text{(Si I = 100 mA)}$ | $V_{s}\,\text{(Si I = 250 mA)}$ |
|---|---|---|---|---|
| $5\,V$ | $10\,\Omega$ | $100\,µF$ | ??? | ??? |
| $9\,V$ | $47\,\Omega$ | $220\,µF$ | ??? | ??? |
| $12\,V$ | $100\,\Omega$ | $470\,µF$ | ??? | ??? |
NOTE : La valeur de C2 sera toujours $0,1 µF$ car les fréquences des perturbations générées par les condensateurs électrochimiques sont inférieures à $1 MHz$.
Une fréquence d’$1 MHz$ signifie une oscillation toutes les $\frac{1}{1\,000\,000} sec$.
D’après la charge d’un condensateur $T = R \times C$; Et en considérant $R$ proche de 1, alors :
\[\begin{aligned} T = R \times C & \iff C = \frac{T}{R} \\ & \iff C = \frac{\frac{1}{1\,000\,000}}{1} \\ & \iff C = \frac{1}{1\,000\,000} \\ & \iff C = 10^{-6} F \\ & \iff C = 0,1 µF \end{aligned}\]
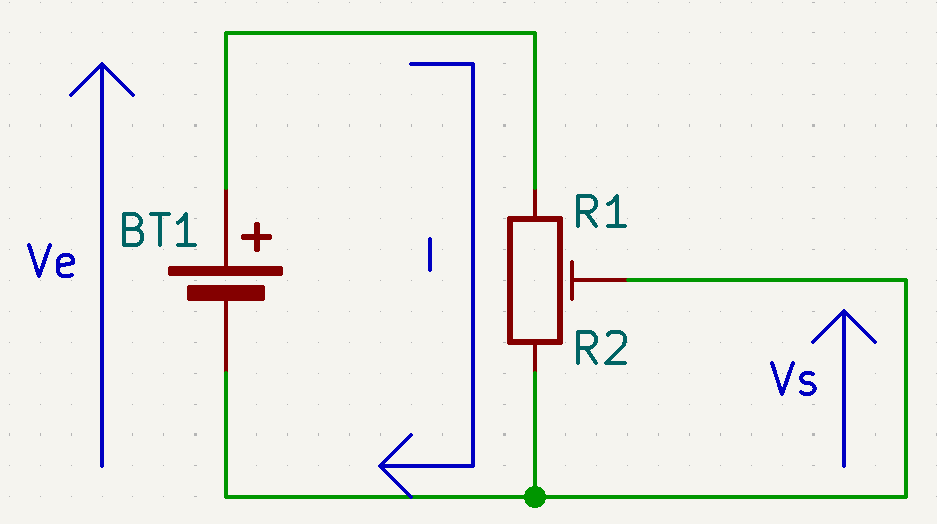
Diviseur de tension
\[\begin{aligned} U = R \times I & \Rightarrow V_{s} = R2 \times I \\ & \Rightarrow V_{s} = \frac{R2}{(R1 + R2)} \times V_{e} \end{aligned}\]Composants actifs
Les composants actifs n’aiment pas avoir les pattes en l’air ! Le principe est donc de relier toutes les pattes, même celles inutilisées (en général reliées à la masse).
CMOS / TTL
TTL plus consommateur que le CMOS. Le CMOS aura les mêmes types de composants que le TTL, en moins gourmand.
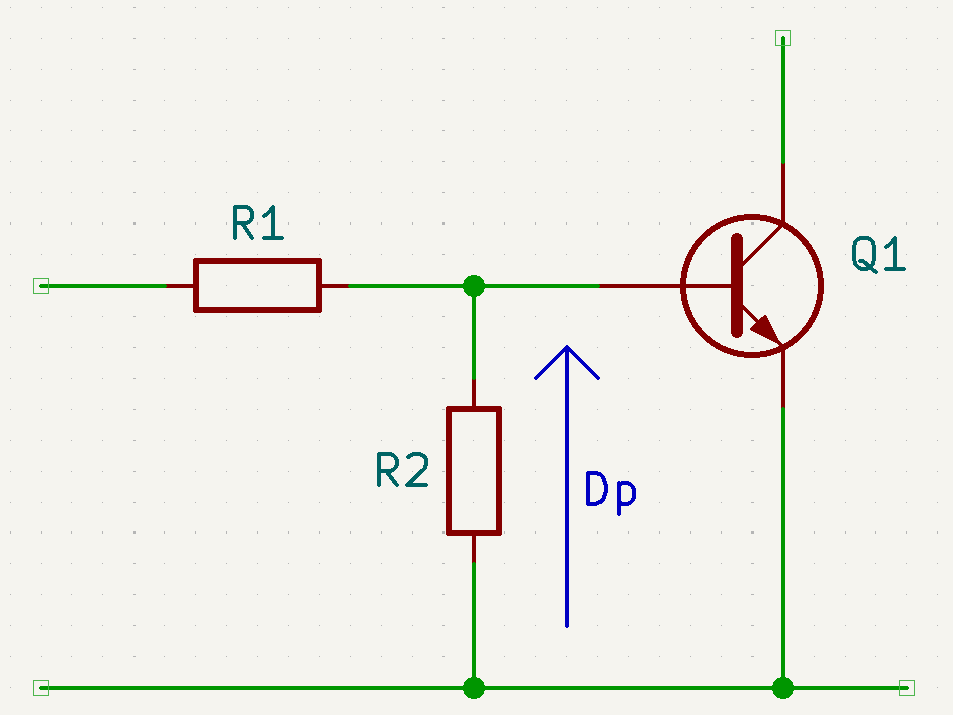
Transistors
Pour un bon fonctionnement, il faut $R2 = 10 \times R1$.
$Dp = 0.7 V$
But de la résistance R2 : Réduire l’intensité du courant dans le transistor.
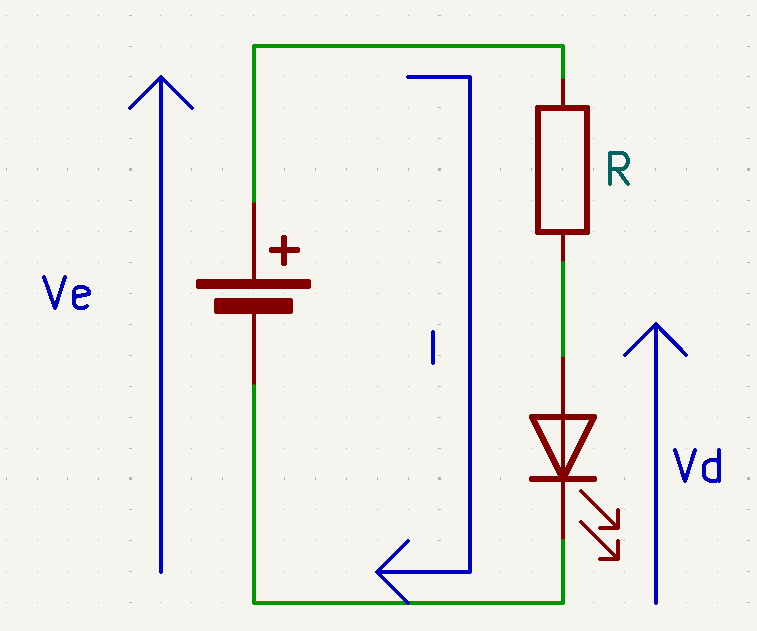
Choisir la résistance pour une diode
\[R = (V_{e} – V_{d}) / I_{d}\]$R \Rightarrow$ Valeur de la résistance en Ohms ($\Omega$)
$V_{e} \Rightarrow$ Différence de potentielle appliquée à la diode en Volts ($V$). Cette différence de potentielle doit être $\ge 1.2V$.
$V_{d} \Rightarrow$ Tension d’alimentation de la diode en Volts ($V$). En générale une diode est alimentée en $1.2V$. Cette tension peut être ignorée si $V_{e} \gt 10 V$.
$I_{d} \Rightarrow$ Intensité désirée pour la diode en Ampère ($A$). En général $5mA$ est suffisant ($10mA$ max).